Gateless Majority Logic

[KD5ZXG]

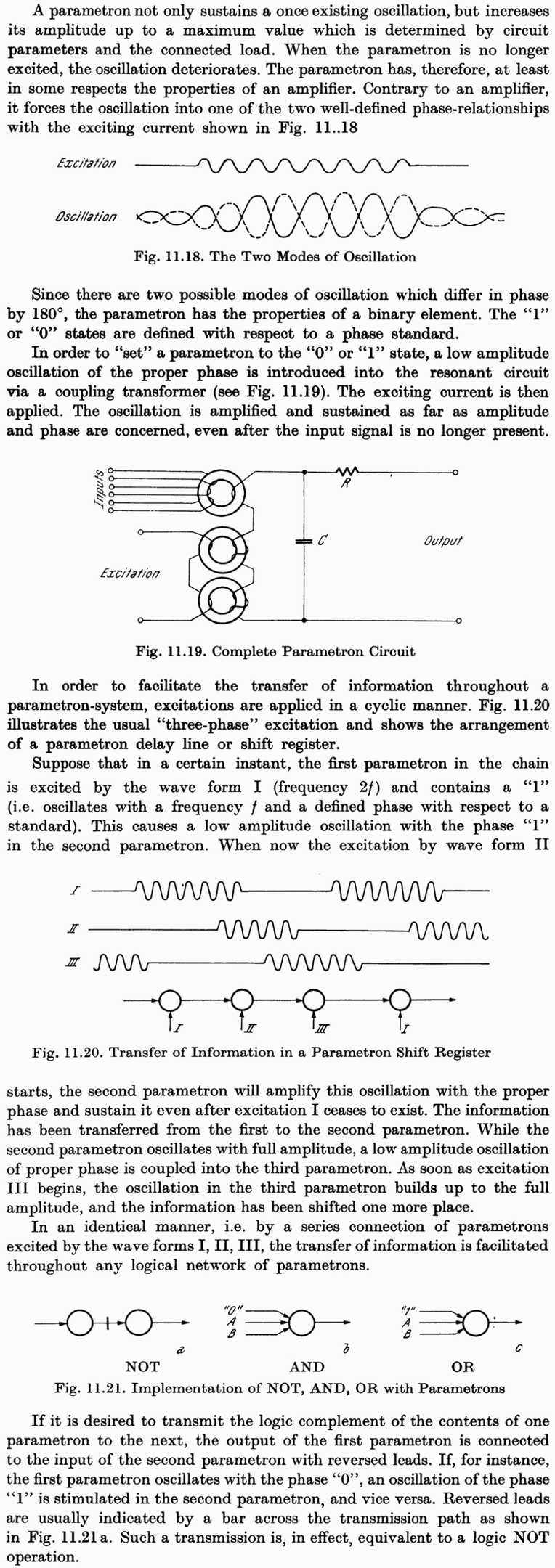
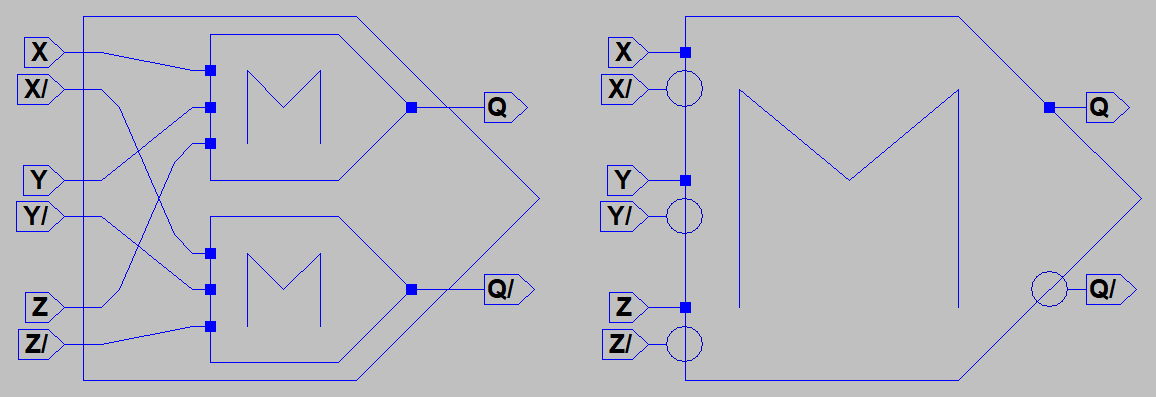
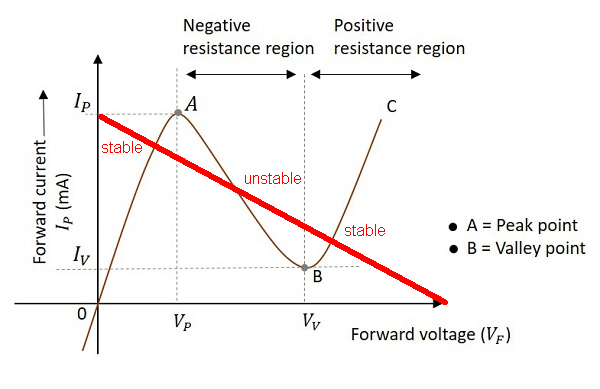
In 1954, Goto Eiichi (Eiichi Goto in English, except he wasn't) developed an oscillating magamp that
could perform majority vote logic, amplify the winning state, and hold the result for as long as needed
in one of two possible phase locks. All without transistors or tubes, just ordinary capacitors and slightly
overdriven inductors. He named this logic device "Parametron".

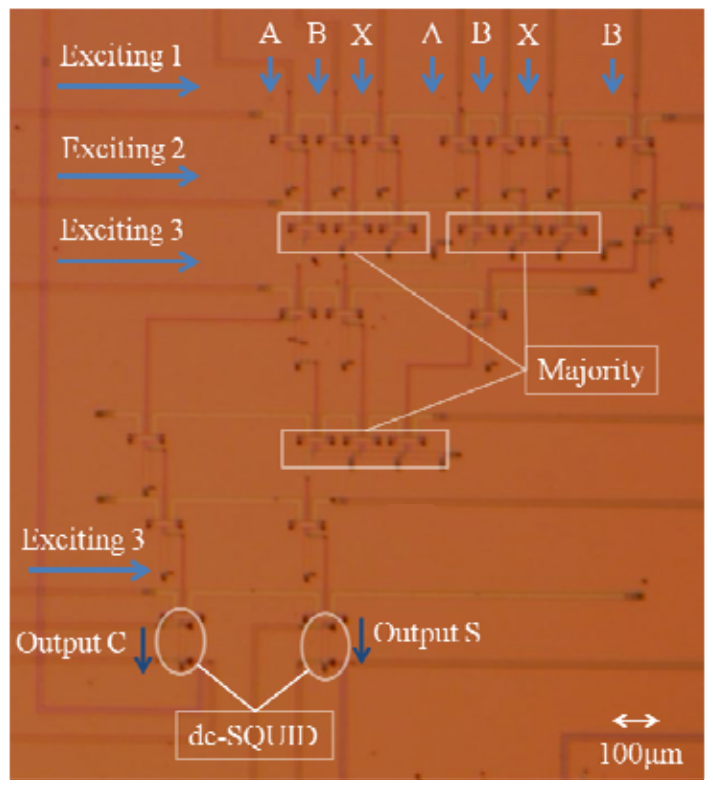
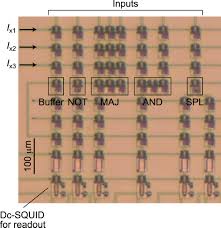
Several early Parametron Computers were built. And from the user perspective, they worked just like
ordinary computers made of gates. NEC put out a brochure for one in English that clearly shows just
how boringly normal these could be if you never looked under the hood. A few tubes were used for
convenience to pump the oscillators, but they wern't doing logic with those tubes. An alternator could
have provided the same pump waveforms for all that mattered.

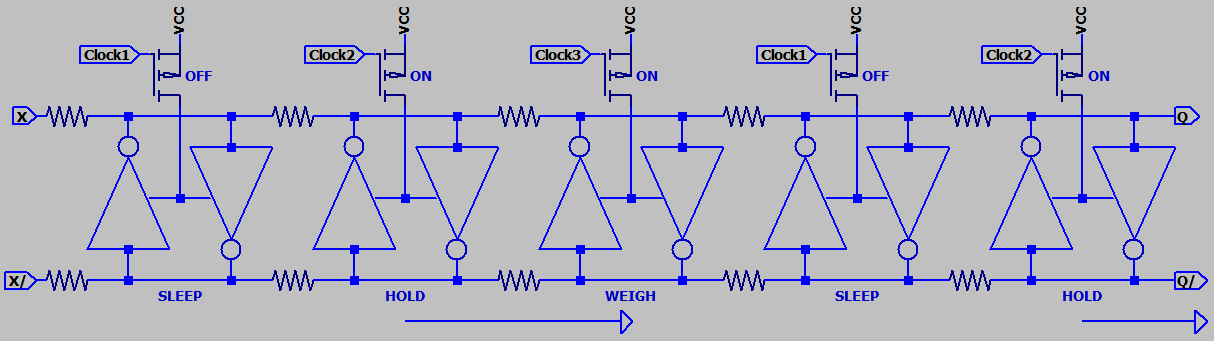
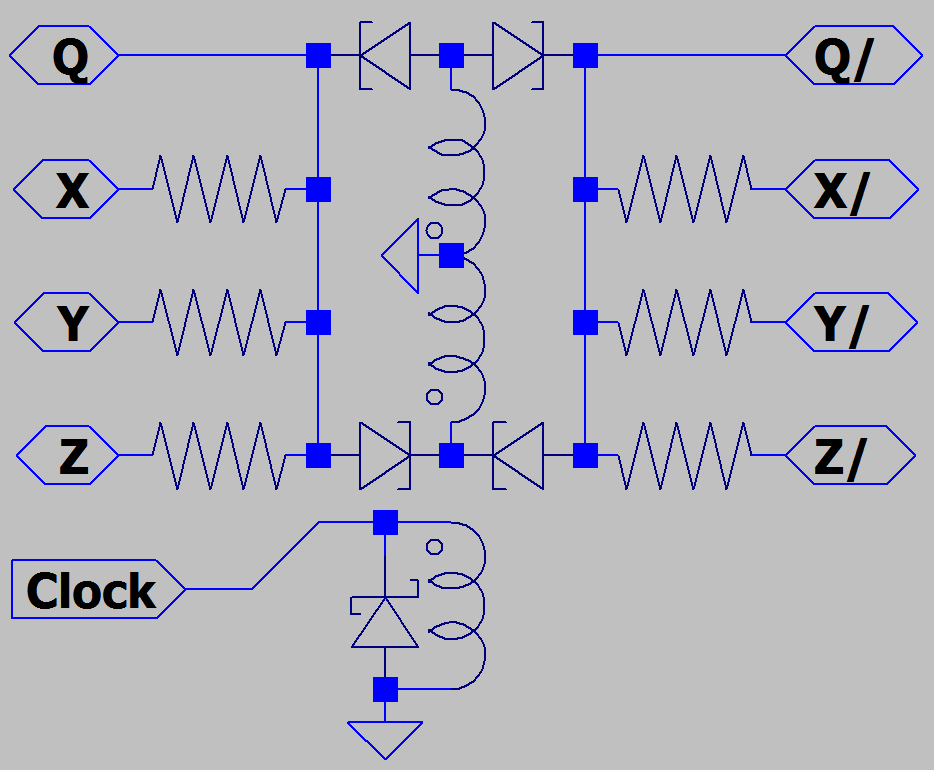
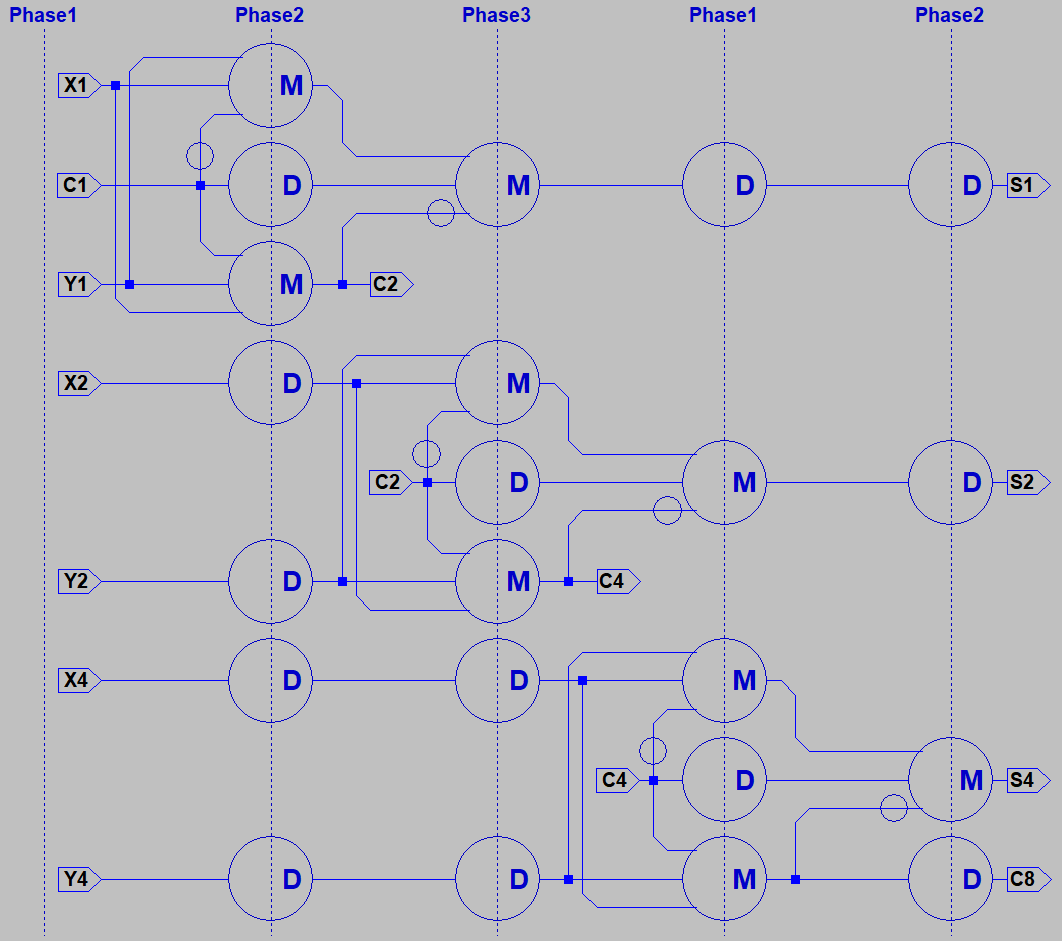
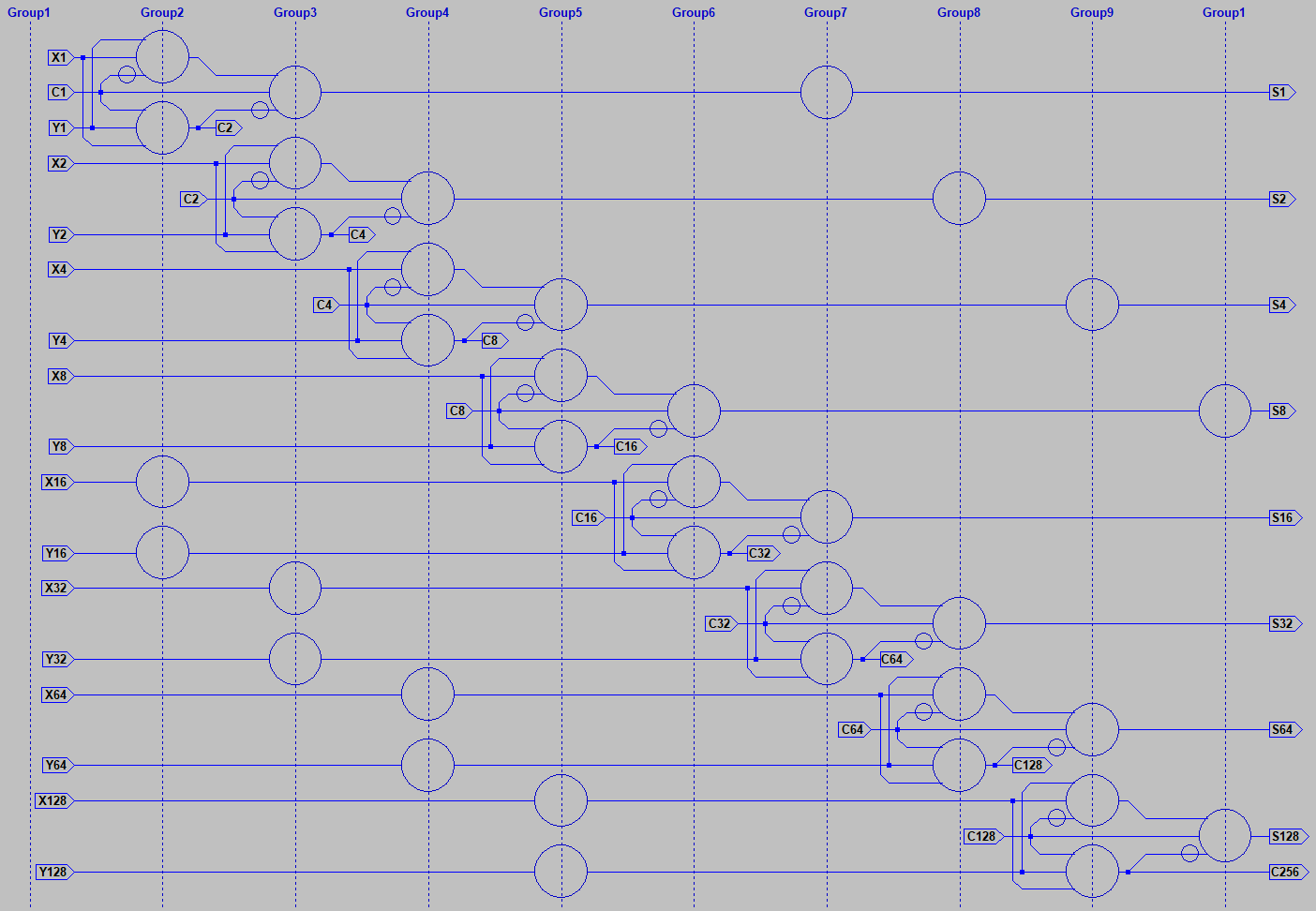
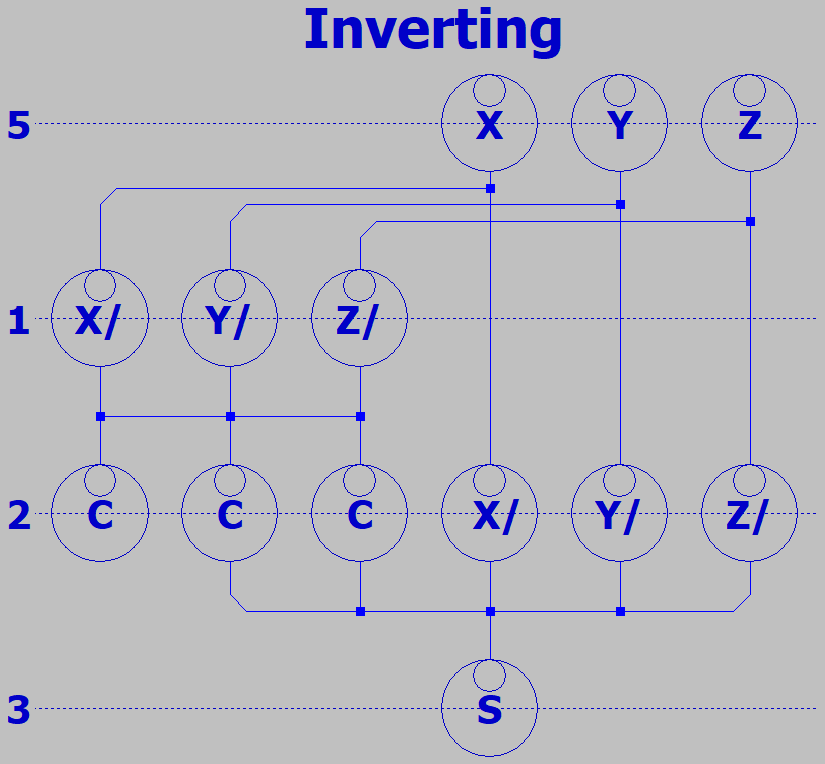
Familiar gates like NAND and NOR have dedicated inputs and outputs. Majority logic is also possible
with gates, but doing so would miss out on several interesting advantages. Majority logic devices were
usually symmetrical, having I/Os without direction. Logic would pulled forward by a three phase clock
that powered down selected banks of devices to forget thier stored state and accept new votes. This
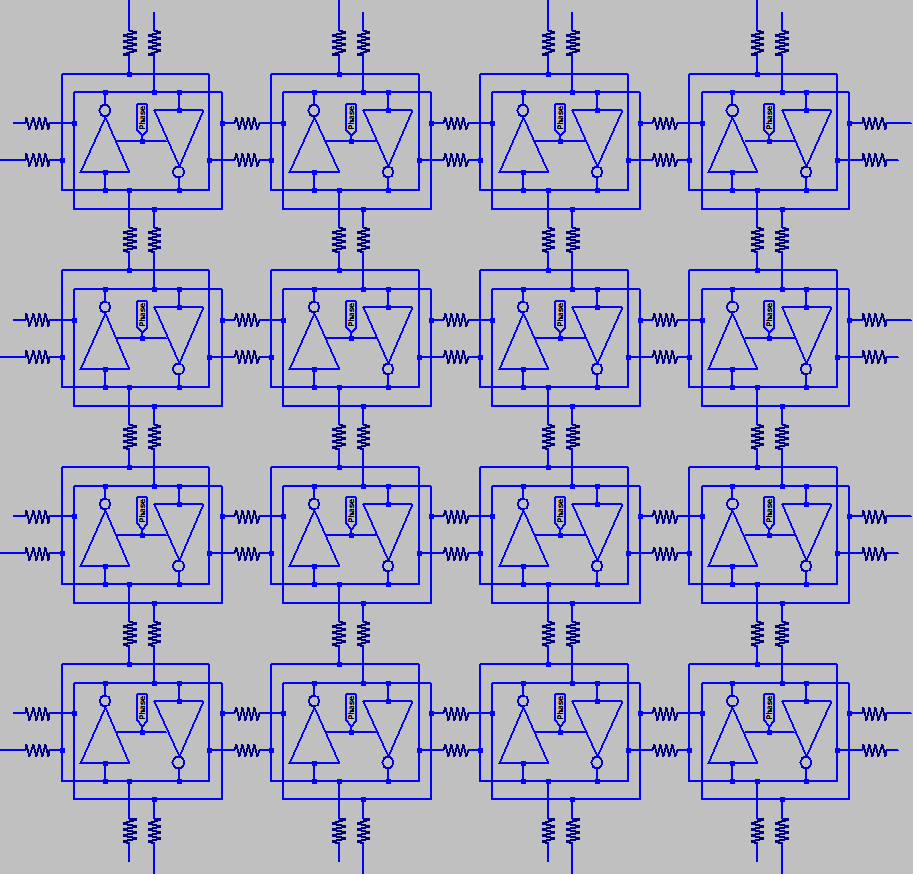
may sound inconvenient, but is powerful important. Because I will show how a programmable array
of such devices can pull logic forward, backward, or sideways...

So how do we compute with majority logic? Well, majority only makes sense if we start with an odd
number of votes, so there will always be an unambiguous winner. You can make a pretty good true
random number generator by having no inputs. But for normal Boolean logic we need at least three
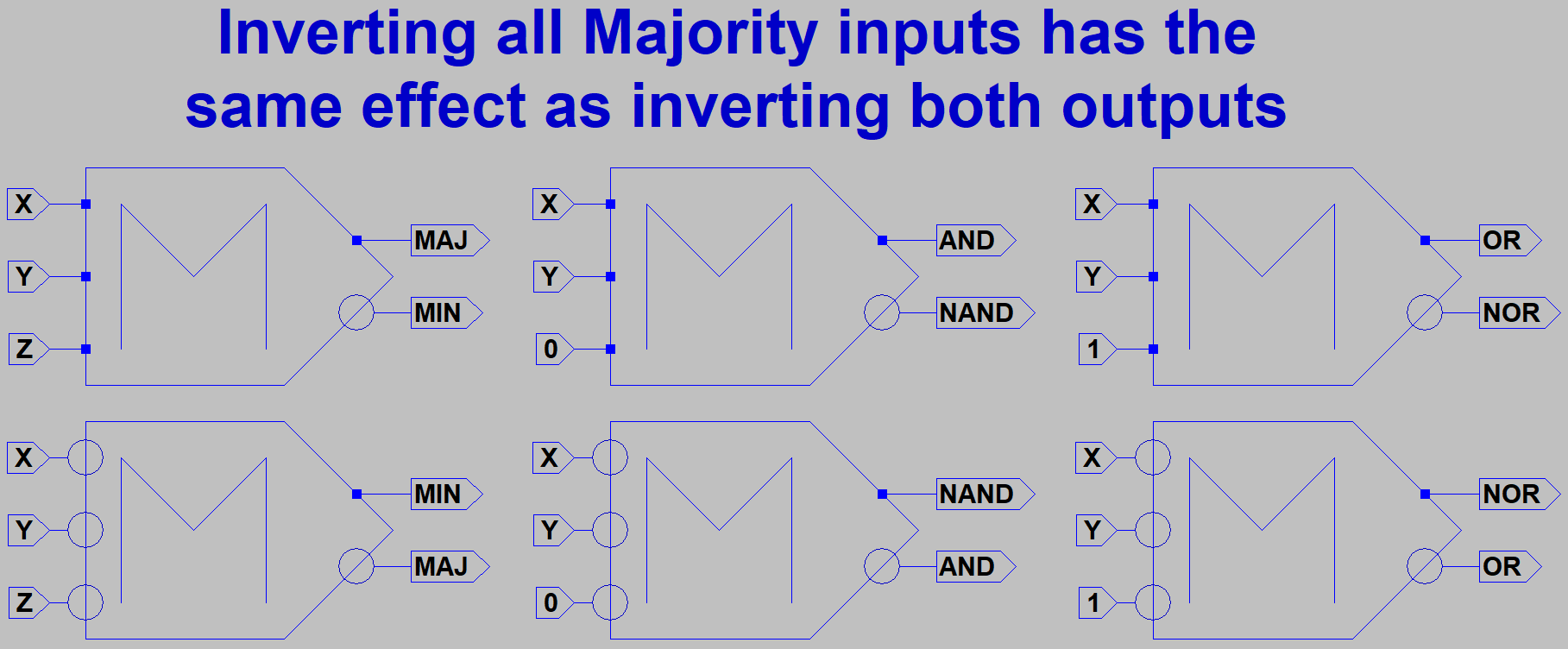
votes. The majority of (1,X,Y) gives the same answer as OR. The Majority of (0,X,Y) gives the same
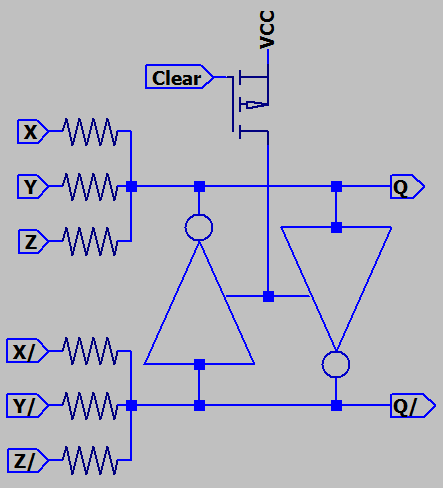
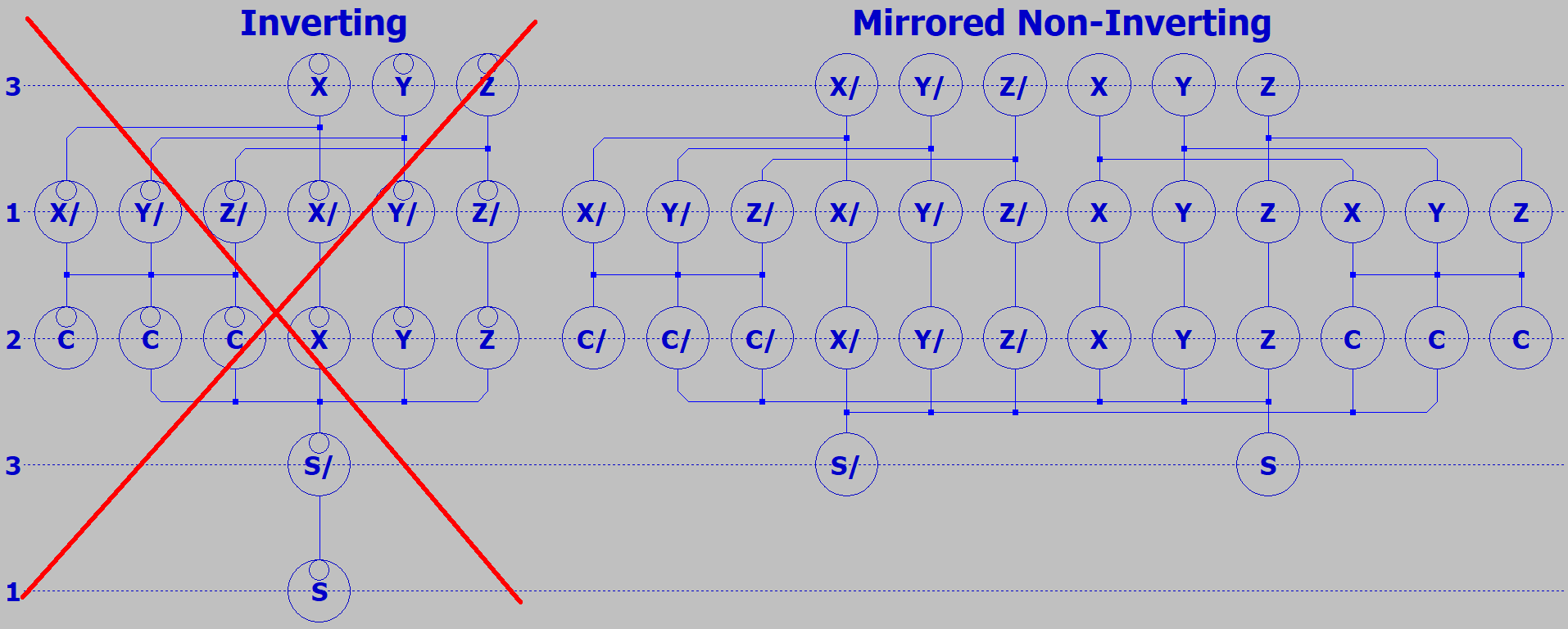
answer as AND. These devices were usually differential, so that NAND and NOR were as simple as
reversing the pair of output wires, giving us Minority Logic.

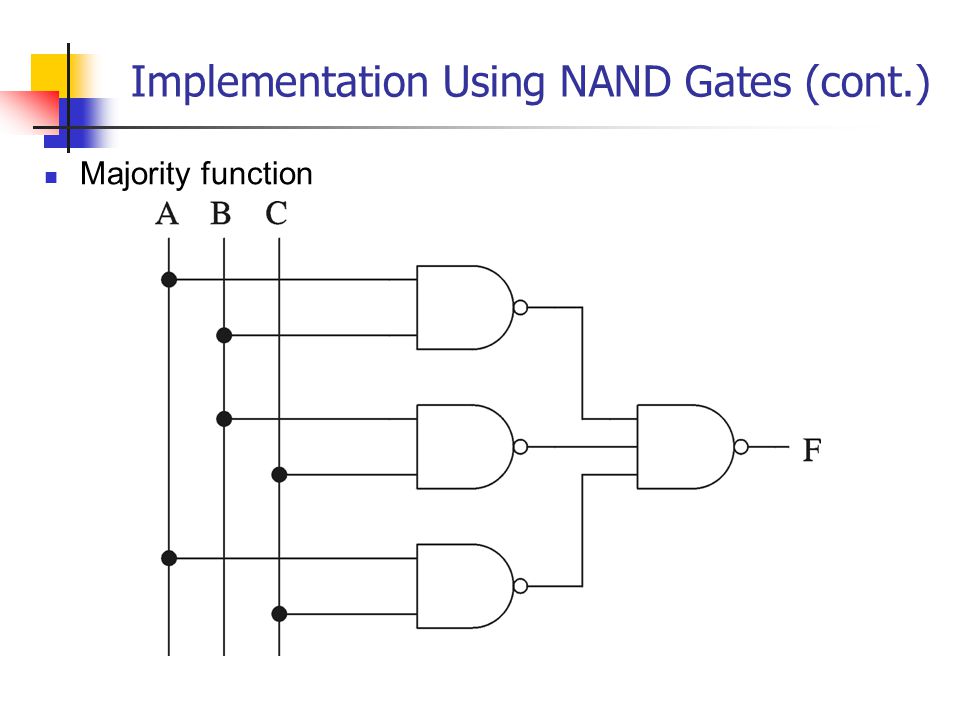
NAND and NOR are universal gates that can build anything. A minority of three gate replaces both.
NOR gates and nothing but NOR gates took people to the moon. Parametrons havn't quite gotten
there yet, though they certainly could have. But looking forward, gated logic is making less sense
as transistors become impossibly small. Directionless logic may become the easier trick to pull off.
Majority of three spins or something, way more than one way to skin that cat. Will even show how
majority logic can be done using only light. Not that light is practical yet, just saying its been done.

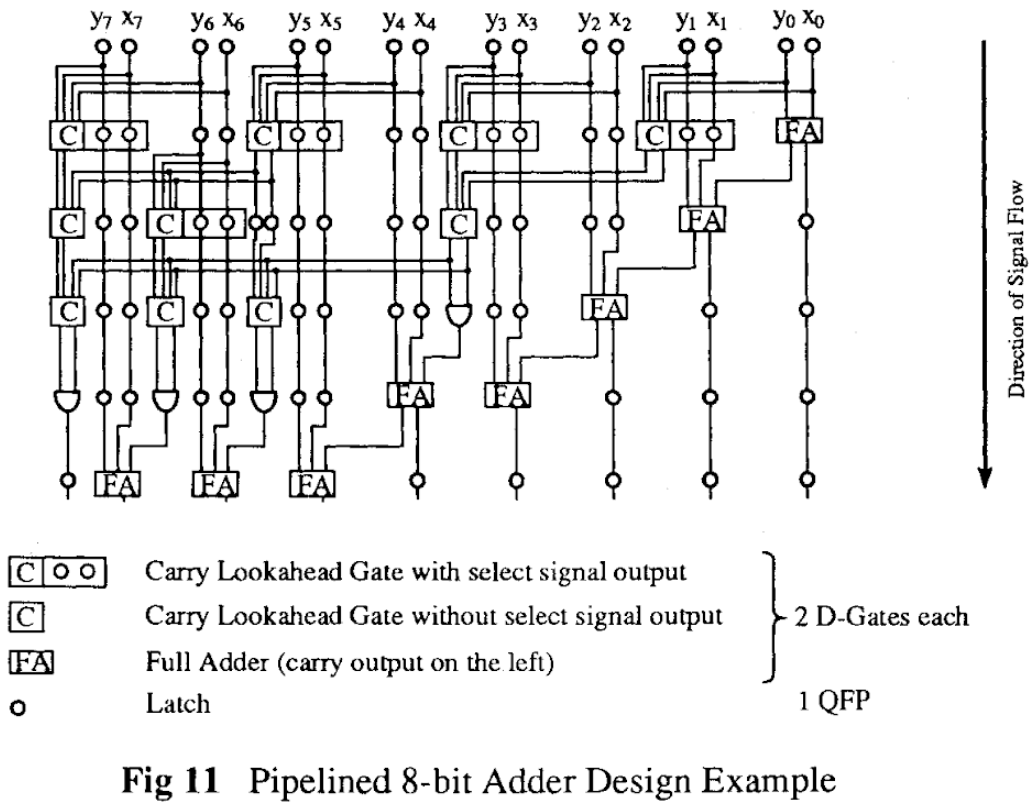
So we got NAND and NOR. Also stores the result like a one bit memory or flipflop. What else can
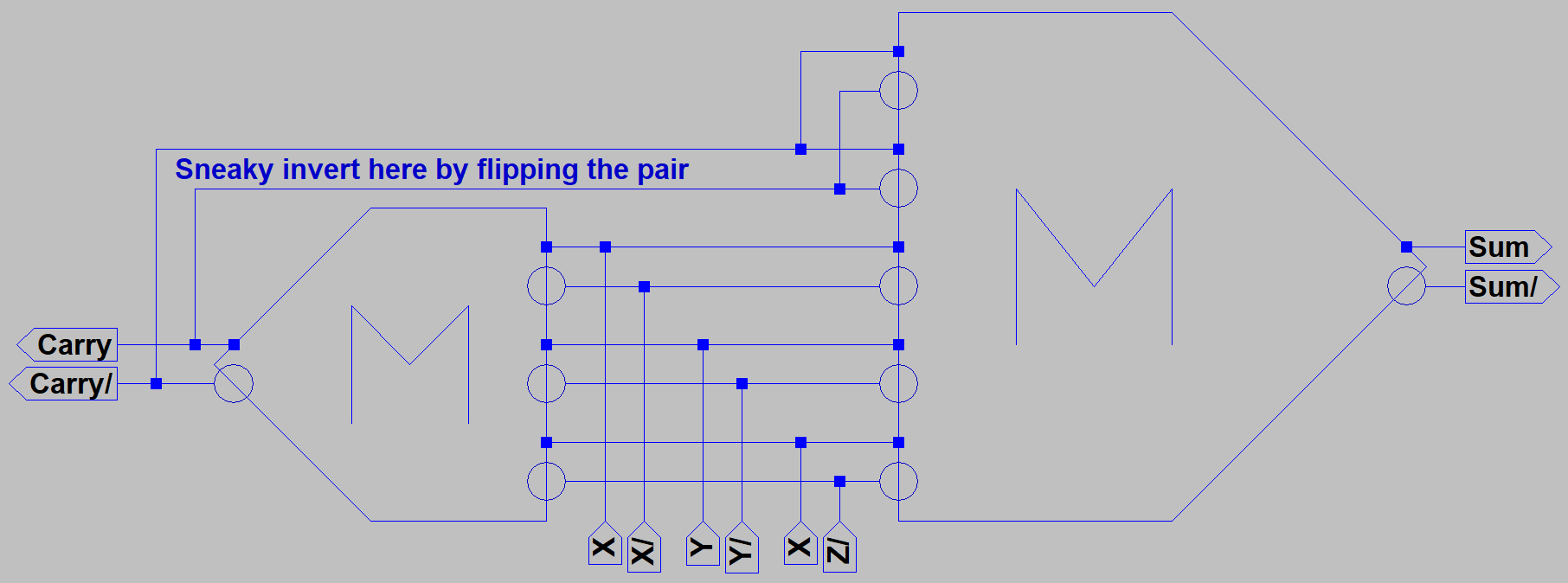
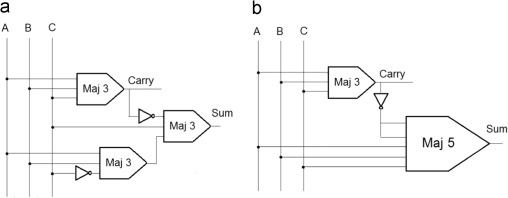
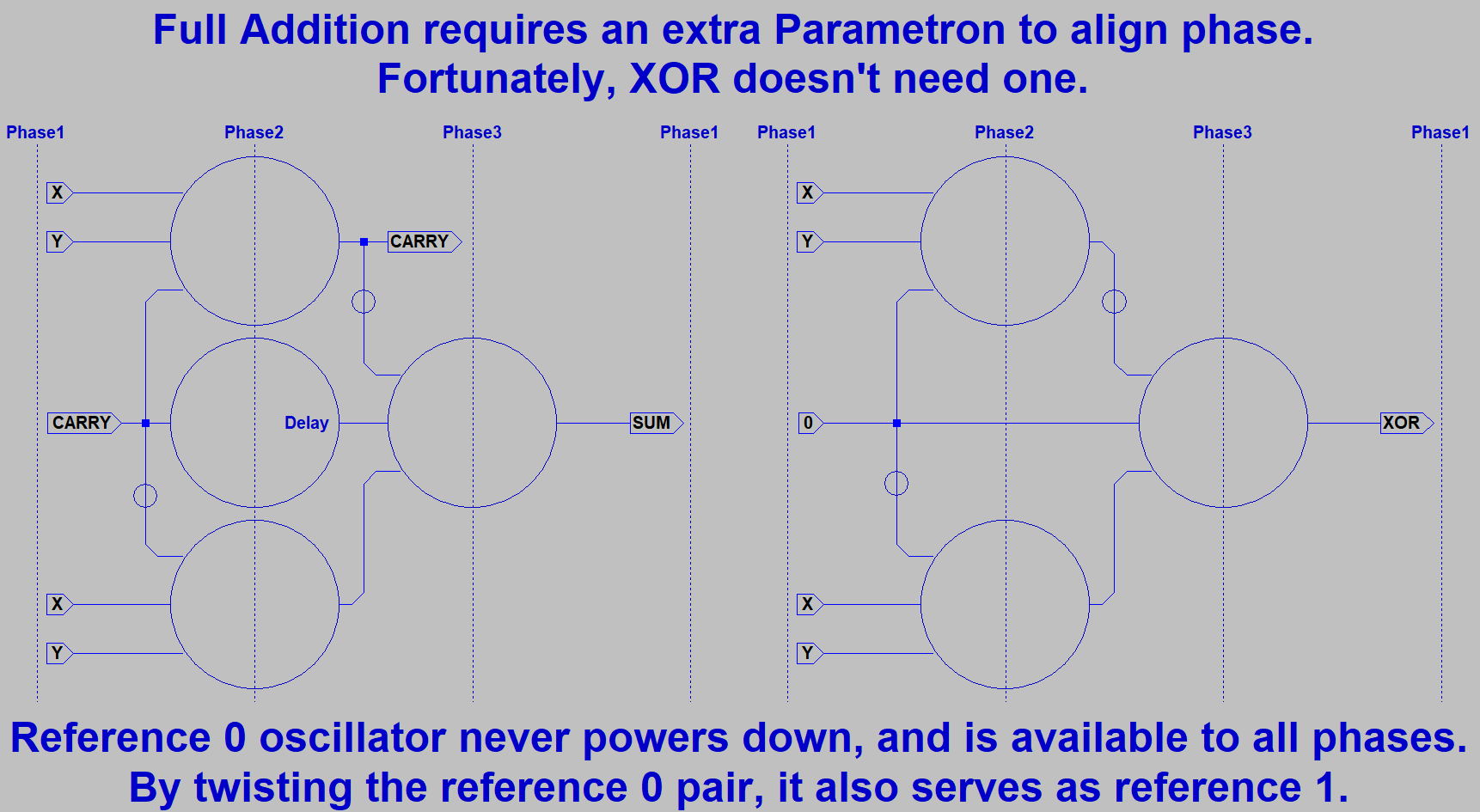
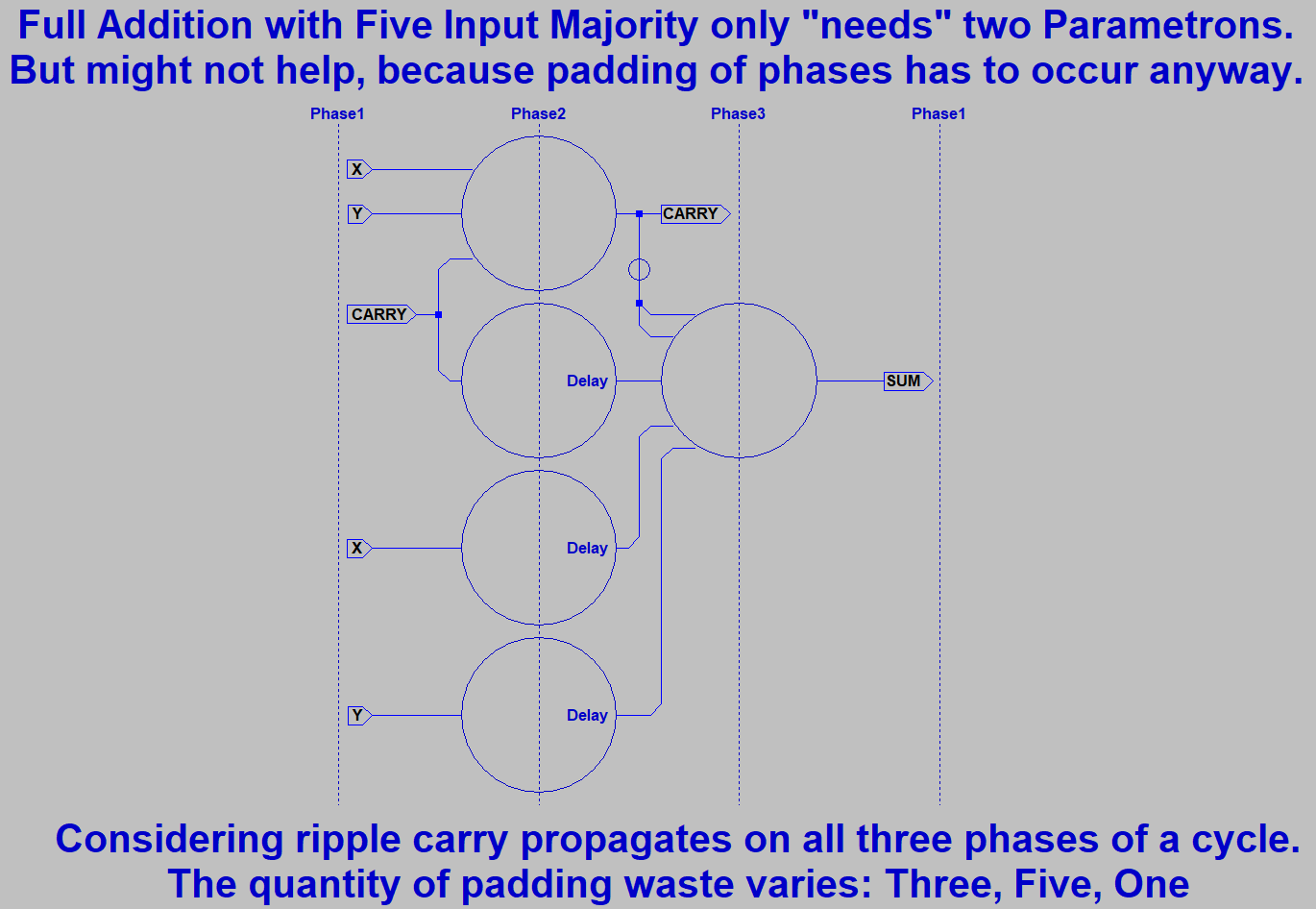
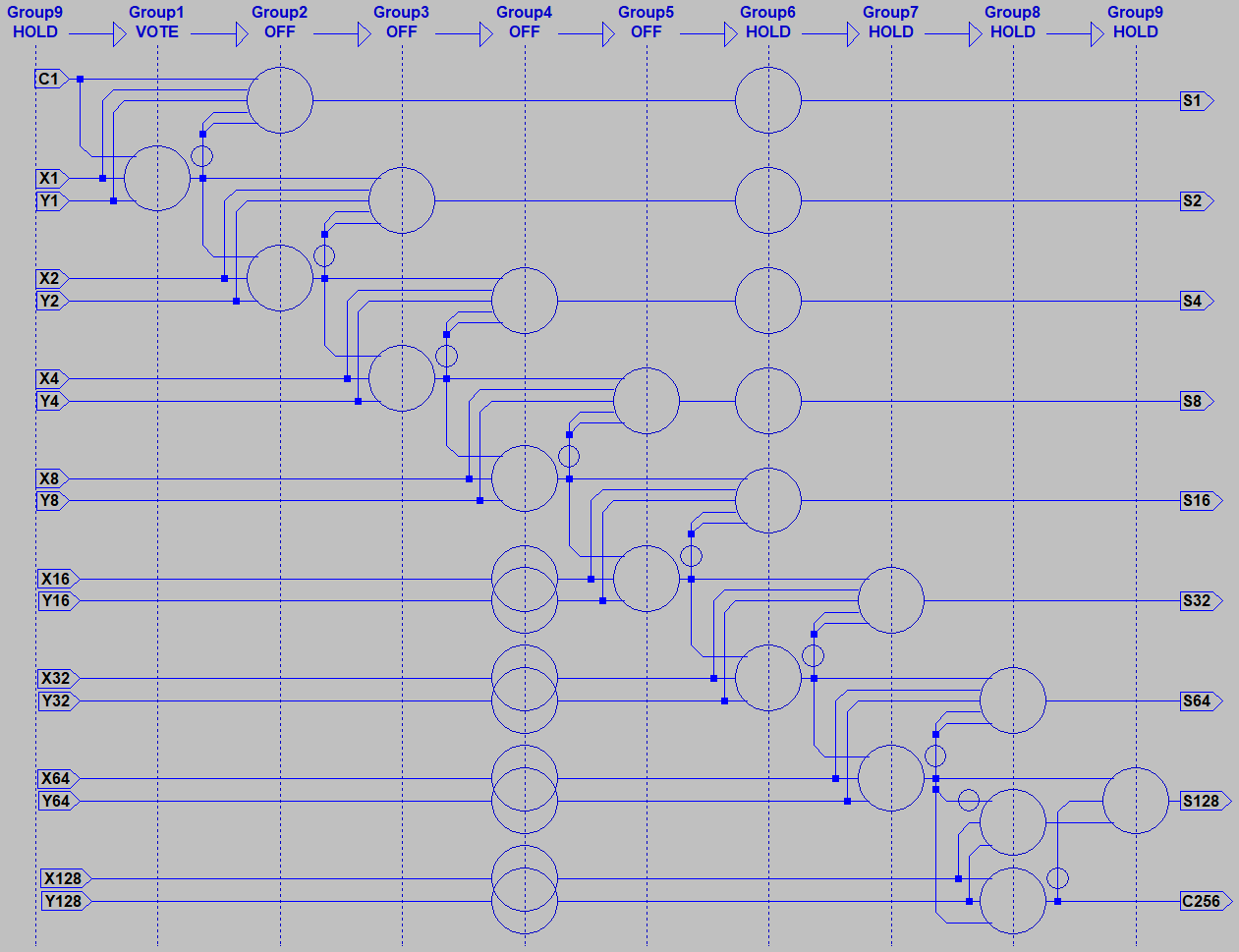
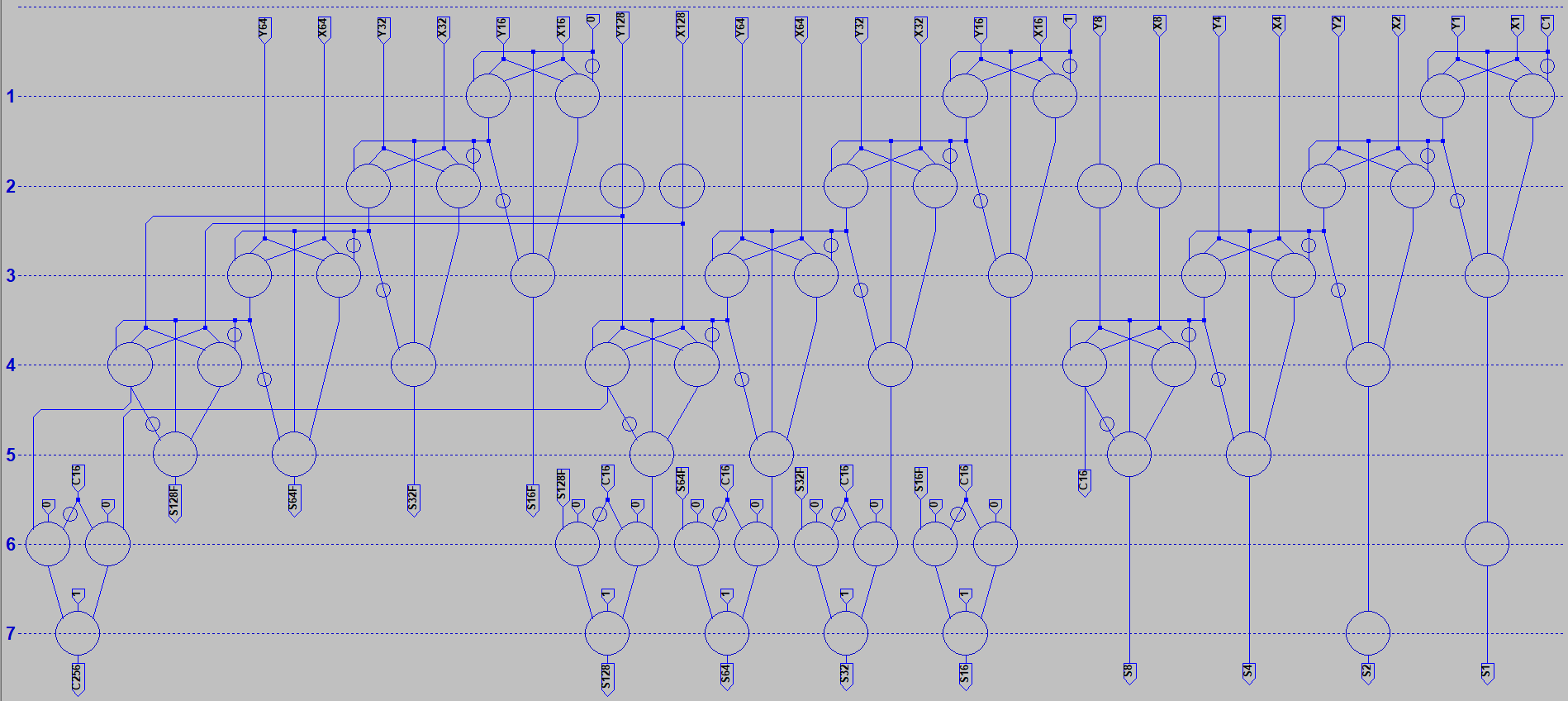
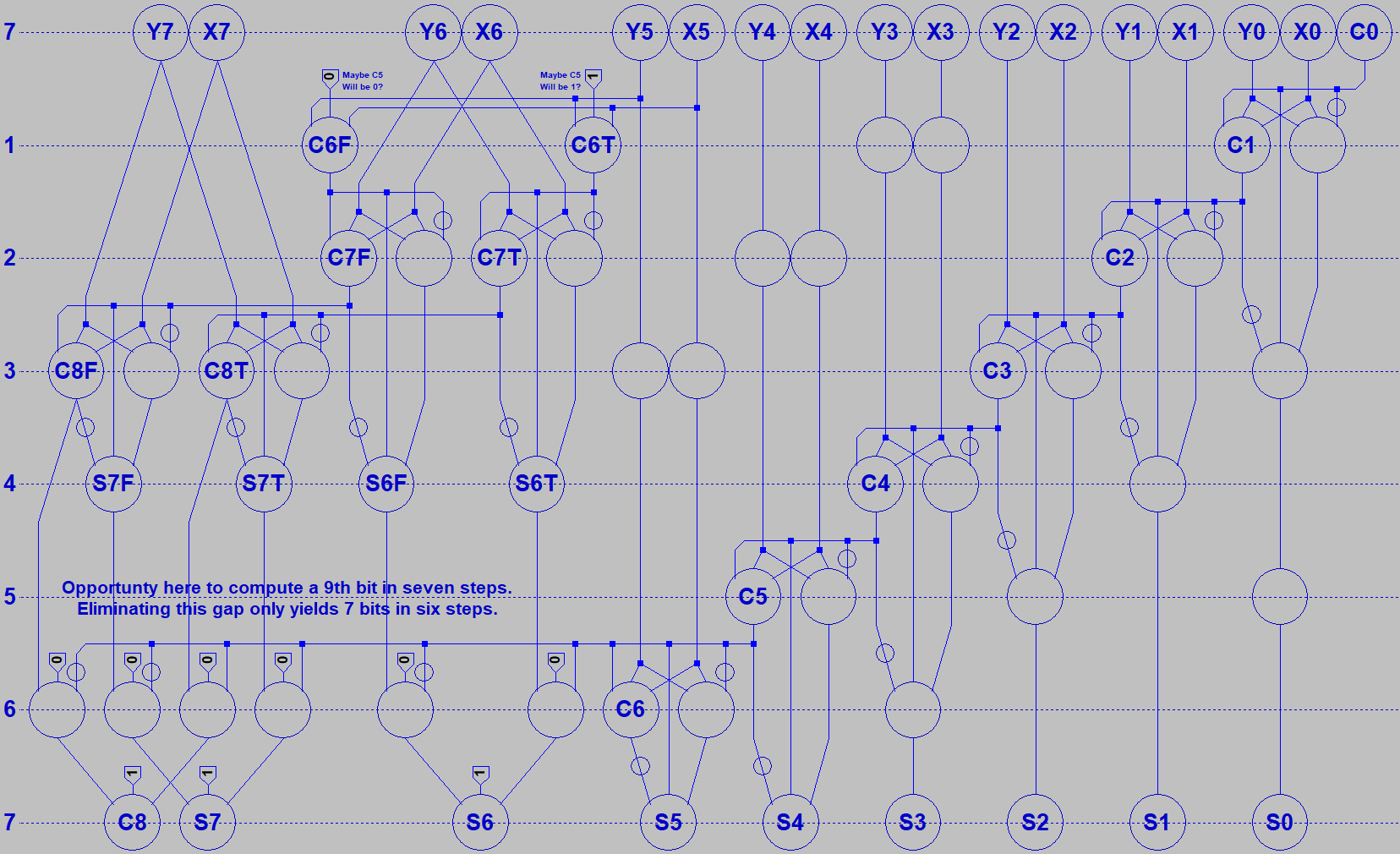
it do? The Majority of (X,Y,Z) gives us CARRY. Cool, so we now have an Arithmetic Logic Unit
that can do a math function or either of two logic functions! Lets complete the ADD function with a
five way vote of (X,Y,Z,NotCarry,NotCarry). Question: How many gates does that usually take???

I'll let you google yourselves up to speed on this, while I gather up the promised attachments.

 

[GoldenTiger]

Ummm, is this homework or something?

 

[KD5ZXG]

If you are having to ask, that means its probably on the test.
Nah, its only if you want to be ready before quantum takes over.

I don't mean the weird cold stuff with entanglements and qbits.
None the less: Minds and faces shall be thoroughly melted.

 

[KD5ZXG]

Lets start off on the right foot by breaking promises.
I said no gates, but have gone ahead and drawn gates anyhow for clarity.
We can mess with the flow of gateless logic after we establish some basics.

This is a full adder in Differential Majority Logic.
We add up the input bits, and if there's a majority, thats a Carry.
We add up the input bits, subtract two carries, and that gives us the Sum.

Two gates vs nine? Might be something to this majority nonsense...
If doing ripple carry, also consider that Carry has only one gate of delay.

To be fair:

With two more NAND, and permit one to have three inputs: Carry delay
could be improved to 2 gates. That improvement would simply emulate
three input majority logic using four NANDs and twice as many steps...

If we disallow five input majority, and had to do it with just three inputs:
It takes one extra gate, and delay is no worse. I didn't choose to begin
with that drawing, because it was less obvious how addition happens.
The drawing on the left below...

But its all a hella lot simpler than all this, cause we won't be using gates.
Before I hit you with oscillators, lets try voting with simple flipflops next.
Then be prepared to throw your comfort zone of a fixed direction of flow
out the window...

 

[KD5ZXG]

Take a break from thinking about it too hard. And take a look at two real
examples of computers built with majority logic, specifically Parametrons...

Be aware: Brochure below is for a different computer than pictured above.
But they are similar enough to put the point across. Completely normal
computers have been built of a logic you might never before have known.

 

[KD5ZXG]

And its not just about the 1950s. Majority logic has been done in pure light.
Look Ma, no gates!!! Ok, so maybe it has a lid. But no gates, no wires, no
transistor. Light doesn't seem small or practical yet, but maybe someday.

At scales so small that transistor gates stop working, majority logic still gets
the job done. Thats why we might spend a few moments rediscovering it.

 

[KD5ZXG]

So, here's a simplified drawing of a majority logic flipflop.
When this device turns on, it will immediately latch to one
logic state or the other. Inputs can vote upon that decision.

But once decided, its stuck with that memory forever.
Further input changes will be ignored. Or at least until a
CLEAR pulse comes along to cut the power and make
it forget.

But what isn't so obvious: The outputs resistively couple to the
next flipflop exactly like inputs coupled from the flipflop before.
The damn thing is symmetrical with four identical pairs of I/O!

What keeps the output from being an input and spoiling the vote?
I will give that answer shortly, just need to draw a new picture.

 

[KD5ZXG]

In classic Parametron Computers, three phases of clock were used to move the logic forward.
Nevermind for now that Parametrons are oscillators and not flipflops...

Sleeping cells forget, and cast no vote (I/O pairs either disconnect or pull to the same voltage).
Votes are pulled into an empty cell as it wakes, only clocks can say which direction is forward.
This shift register would work just as well backward, if the clocks were phased that way...

 

[KD5ZXG]

For a big mess of wires that go exactly where they need to and nowhere else, three phases suffice.
Post #5 shows us two perfect examples of partially wire directed flow that used only three phases.
But might be handy to have more than three phases to pull logic through an array where the wires
are fixed only to neighboring cells. Each cell would be programmed to sleep on specific phases.

Because input and output occur on different phases, any cell of this array could have as many as
four inputs, and on the next phase as many as four outputs. Though all connections drawn here
are non-inverting, obviously sometimes signals will need to invert. Maybe we could add diagonal
connections, and let those invert...

Oscillating Parametrons had a constant reference zero that could be hardwired, or wire-inverted
to a 1 wherever needed. That method might not be suitable for an array of flipflops on a chip.
But each cell could be made slightly unbalanced, such that a tie always results in a constant.

The array could be haxagonal instead of square, no problem. Also nothing stopping us from
stacking multiple layers and pulling the flow of logic around in 3D. Having at least two layers
neatly solves the issue of allowing signals to cross each other...

Might add a few axons, so signals can reach remote places faster than taking Conway's glider.

We ain't trying for a slow propagating cellular automata using only local dendrites, nor a big
mess of wires with only axons, but something sensible that leverages the best of both.
In the end, anything practical will have to be a mix of programmed and prewired flows.
For programming majority arrays in VHDL, let how it flows be the compiler's problem.

 

[KD5ZXG]

The magnetic energy stored in an inductor is one half of it's Henry rating times the current flowing through it squared.
E=0.5*H*A*A. You don't need to memorize that equation...

If we reduce the Henry parameter while a current is flowing, that current tries to increase. When Henries go down,
Amps go up. Because energy freewheeling in the inductor's magnetic flux prefers to remain about the same...

If we build a tuned circuit consisting of a capacitor and variable inductor, its not just gonna start oscillating all by itself.
But any small voting current in that variable inductor, perhaps even random noise if no vote, can be given a kick by
periodically reducing Henries. And those currents can build up to a full scale oscillation. Now you have a Parametron.

The most effective timing is to pull back Henries twice each cycle of oscillation, so that the tuned circuit picks up
current both coming and going. Eventually amplifiying swing to full scale, and locking onto 1/2 the pump frequency.
But we could swap going half cycles for coming half cycles, it would amplify and hold that oscillation just as well.

And that is the difference between a stored one and a stored zero. Could lock onto the odd pump cycles, or the even
pump cycles. If we listen to the resulting zeros and ones, the same as audio data stored on some early casette tapes.
Binary Phase Shift Keyed.

Next post, we cover a way to reduce Henries on demand. And with pics that will hopefully make better sense.
Some extra confusing side notes first...

-----------------

There are other parameters we could twiddle: Variable capacitors can give a boost to Voltage when Farads reduce.
Same way a condensor microphone works E=0.5*F*V*V. We wouldn't build an oscillator out of mics, that would be
kinda useless. Variable capacitance across the depletion region of a diode has sometimes been paired with a fixed
inductor...

Or the optical table I showed earlier, with a nonlinear piece of glass. Pump it with blue laser, and excite an infrared
oscillation of half frequency. Don't know the actual color used, just imagining blue. Its called a "Degenerate Optical
Parametric Oscillator". Degenerate in this case meaning it has only two possible phase relationships. Not exactly
what degenerate usually means around here.

Compare the phase of two of these, and you have an excellent true random zero or one, that holds until you turn it
off and let it forget. Parametrons are excellently balanced to amplify a true random from noise, not like flipflops that
tip predictably on no-input.

 

[KD5ZXG]

Julius Sumner Miller, or Scanners? You decide...

Had to replace one of the videos cause an old link went dead.




Glorious, now the other video went dead.

 

[KD5ZXG]

Alright, picking up the pieces from where our heads exploded...

You might note a strange pair of toroidal transformers labeled "Excitation."
Those two are wired to buck each other and produce no transformer action.
The puprose is to overdrive (saturate) those donuts and reduce inductance,
without acting like a transformer. Actually its acting like a magamp.

Inputs and outputs can be coupled from the same donut. I dunno why the output on
the right was directly coupled, except it doesn't matter and saved a few turns of wire.

----------------

Example below I built as a random number generator, without inputs.
One coupling donut shy of what you read about in the paper above.
I also ran DC bias on a solid wire, separate from 2f excitation (blue),
which proved an unecessary feature that didn't make any difference.

Solder blob on the right is the midpoint where the two donuts connect to each other.
You might expect that to be in the middle of the picture, but I had to work with wires
that were already glued to the donuts. So they are not mirror image of each other.

Now, where the gate???? Ain't none, except maybe three for shutting down clock lines.
A clock line might then be shared by several parametrons of the same timing group.

But we don't even need gates for clocks. Imagine a pair of mechanical alternators
spinning at slightly different rates, and evenly mix those outputs. They will reinforce,
cancel, reinforce, cancel, reinforce, cancel, and create the required clock waveform.

Reading the output phase was sometimes as simple as a neon bulb wired between
a known reference zero and an unknown output. If they were enough different, the
bulb would light. Neon wouldn't light at low voltage and screw up a vote that hadn't
yet been amplified to full scale. A shift register like that might make a cool clock,
like the kind you might hang on a wall...

-edit-

I've since come to wonder if DC bias might be replaced by permanent magnets?
Would solve a complication of transformer coupling between bias and excitation.
Cause I need a better choke on DC than offered by just two long beads shown.
It worked anyway, in spite of the unintended cross-coupling.

Old school solutions might have been to generate AC and DC together as the
output of a high impedance amplifier. Likely the plate current of a few tubes.
A method to silence the three exciting lines in clock sequence also solved.

 

[KD5ZXG]

Majority logic can be built of an amazing variety of things, including gates but not limited to them.
Once you get your head around it: Majority logic could easily be made of out of water, golfballs,
light, single electrons, memristors, magnets, quantum dots, tunnel diodes, the list is just endless...

But not all ways of performing majority logic are inherently differential, nor do all of them provide
minority logic, or inversion. Except thats not an actual problem, you just have to know the trick.

If I build two single-ended non-inverting majority gates and operate them in parallel: Such that
one operates on inputs (X,Y,Z) , while the other operates on inputs (X/,Y/,Z/) , the combination
provides exactly the same outputs as a differential gate. Which means we can simply swap
signal wires anytime inversion is needed for free, with no delay. No need for any real inverter.

I tend to prefer differential for electronic implementation, because the tipping threshold sets
itself reliably without need for tweaking. Single ended implementations make more sense as
one gets smaller, where thresholds become reliable properties of physics. But might need to
lean on the parallel trick, when no better way of inverting easily presents itself.

 

[Red Falcon]

Loving these posts and information.
I haven't read through everything yet, but hot-damn, this is some great information.

Thanks a ton for sharing!

 

[KD5ZXG]

Parametric amplifiers and oscillators are also useful for receiving weak signals from distant spacecraft. Inductors
and caps have a lot less noise than transistors. Signals in good phase with 1/2 the reference pump are amplified,
everything else attenuated. It can really clean things up.

http://www.gazettetimes.com/news/lo...cle_766dfc5a-c8da-5440-a6fd-50c8c1b6909e.html
Only 10 years ago, we might have asked the man himself. Since he's no longer giving lectures, I will put on
my magic 2f tinfoil hat and attempt to channel some Engelbrecht. Too bad I don't dress quite that sharp.

Im just assuming, not 100% sure, but those diodes of his were probably reverse biased such that they did
not conduct. His objective was only to voltage vary the capacitance parameter and pump-up an AC signal
as it passed. Possibly two signals (transmit and recieve) simultaneously travelling in opposite directions.
Not to make noise like a typical forward biased junction, and also why a transistor wouldn't have helped.
-edit- 2f exciting waves can also travel along with the wave being amplified, this method is unidirectional.
Not clear from photo above whether that thing was setup to amplifiy both directions or just one...

The small signal gain of a parametrically pumped amplifier is exponential. A certain minimum size signal and
minimum size kick from the pump have to occur together on time to merit a gain greater than 1x. If we have
enough signal, a pump with compatible timing, and feed output back to the input, we can make an oscillator.

Small signal gain is exponential, does not mean large signal gain is infinite. If energy of a signal tries to exceed
that of the pump: Would not be amplified, but would spill backward into the pump, so the system is self-limiting.
The strength of a vote is amplified to a consistent output level, regardless how many or few inputs voted.

If we tune slightly off 1/2 pump frequency, small signal gain is reduced. Sometimes useful if you don't want
random noise or excessively weak vote to automatically build up to an oscillation. Signals that aren't already
loud enough to merit gain, even if they have close to proper timing, quickly decay to nothing. This can make
a third quiet logic state, though not exactly an open circuit the same as "tri-state". May not be oscillating yet,
but connected and listening, even to the outputs. Ready to trip on any loud enough glitch that might be heard.

This relates to logic if you want a Parametron that self-starts from noise as a true random number generator.
Need to make sure the pump is strong enough, and very close to 2f in-tune, that even the noise floor merits
gain 1x or greater. Else your random generator will do nothing but look at you like you stOOpid or something.
Mine has 10 turns of blue wire pumping at 2f, not cause I originally planned to need that many. Parametrons
with reasonably strong logic inputs, might only need excitation by one or two turns of the pump to get started.

Randomness can be improved by using a pair or more in XOR to cancel outside influences that might have
nudged them in common. 100% sure there was a patent where some dude had done just that with a pair of
optical Parametrons.

Too bad I don't dress this sharp either. Just watch where you point that thing...

https://en.wikipedia.org/wiki/GR_connector

 

[KD5ZXG]

Don't quite get what all the extra junctions are for in this adder, unless maybe for doing the parallel trick.
Perhaps they fudged subtract into the circuit too? Anyways: this is a Quantum Flux Parametron (sadly, no
Flux Capacitor) made of superconducting Josephson junctions, whatever the hell they are. I'm not gonna
be digging into this option too much futher, cause it seems to need an absurd amount of cold to work. But
its an impressive Japanese effort to carry on the work started by Eiichi Goto.

Quantum, but functions not as some weird quantum computer, just a really fast regular computer.
These things are actually useful in weird quantum computers too, if only for detecting the outputs.
They also claim low power, like almost none. But I want to see the bill for running that fridge 24x7.

Whats going on these days with Memristors and Logic-in-Memory should be of much sooner use
to real people that live & operate at room temperature, or slightly above. Maybe we go there next...

 

[KD5ZXG]

Well, after way too much reading I still don't understand memristor logic in memory.
Clear only now: While a Programmable Majority Logic Array still seems possible, the
memristor people have been working towards something entirely different. An Akers
logic array. Shamefully, I just don't get it. Maybe that bulb will light for me later...

So next majority logic: I think might be Esaki Tunnel Diodes arranged in Goto Pairs.
A quantum logic of the 1960's you probably never head of. Nothing weird going on
here, unless you consider the topic of "Negative Resistance" to be weird.

There is no such thing as "Negative Resistance". Ordinary Resistance = Volts / Amps.
And this plots a straight line with a fixed slope. But a Diode can have a curved slope,
possibly with dips. All points on that curve will have a positive resistance if looked at
individually. But a dip midway in a rising curve may present a range of negative slope.
"Negative Differential Resistance" definitely does exist, and sometimes damn useful.

Shockly (inventor of the four layer diode, but more famous for stealing credit from his
assistants who invented the point contact transistor) was maybe first with a solid NDR
diode. (NDR had been done before with tubes.) But he never tried Majority logic that I
know of. Shockley's diode was a bit slow, and ate a lot of power. You can kinda fake
one by hooking up an old metal can 2n2222 the wrong way. It works, just not real well.

They gave Reona (Leo) Esaki a Nobel prize for his tunnel diode. It was quantum fast,
and used very little power. So yes, very damn useful. And Goto put them to immediate
use in pairs as Majority Logic devices, obsoleting his own Parametrons for decades.
Parametrons did eventually made a quantum comeback, but that was only recently.

Unfortunately, NDR diodes were not exactly brain dead obvious how to use. And very
difficult to manufacture with 60's tech to any consistent specification, leading to a mess
of bins with incompatible thresholds. These days, you will probably only find them in the
trigger circuit of oscilloscopes, radar guns, and Russian military surplus. Was death by
unpopular=expensive, not by any technical problem that couldn't be overcome.

Schematics and pictures next post...

 

[KD5ZXG]

A normal resistive loadline plotted against an NDR would cross at stable operating points
just to the left of A, and also just to the right of B. Also somewhere inbetween A & B there
is a third operating point on the NDR curve that is totally unstable. From here, it will snap
to either of the stable points at the first opportunity.

Imagine a loadline drawn from about where this slide sais "Ip" to about where it sais "Vf".
Nevermind, I edited the picture so you don't have to strain your overworked imaginators.
Actually, Goto Pair is vs another NDR diode's mirror image curve (flipped left/right). So,
you can imagine how those curves might cross instead, if you are up for the challenge...

Voting at quantum speed only helps if you can forget old obsolete votes just as fast.
Abusing a slow transistor as a *GATE* to interrupt power would defeat the purpose.

So we need a way to pass and shunt AC power that comes from a gateless oscillator.
I'm thinking maybe a Magnetron ripped from a microwave oven? Roughly 2.45GHz.

The patents all seem to leave out the details of how the power clock was distributed.
I suspect because that problem was never completely solved. I don't think to built as
oversimplified in my drawing. It probably wouldn't work too well, if at all...

The second issue, which isn't a problem, is that the results of this vote non-invert.
So we lean on the parallel trick, with a whole redundant machine dedicated to an
alternate, quite possibly evil truth. Kirks get swapped whenever inversion needs
to take place. Instead of Q and Q/, should those outputs have been K and K/ ???

Back to reality for a second: The Goto Pair still needs explanation. It latches up
or down, because both NDR diodes refuse to operate on the negative slope of
any answer inbetween. In the case of Esaki tunnel diodes, that slope is due to
quantum tunneling across a PN junction. The junction is never driven to the full
forward bias of a normal PN diode, so we don't have any slow turn-off behavior.

And a third problem, solved in drawing, but totally forgot to explain till just now.
Two thresholds fixed by tunnel diodes do not compare across the differential.
This has only fake differential, so a vote cannot be nulled by pulling a pair up
or down in common mode. Both must disconnect, or both pull to the middle.
I chose pull to the middle, perhaps also disconnect by virtue of insufficient bias.

Clocking this way causes a fourth inconvenience. That it can't and won't hold
a result forever. Results need to move on before clock transformer saturates.
A persistent memory bit would then require a loop of three such logic devices.
Or rely on DC power and a gate to turn off, which brings us back to square #1.

There is no evidence I've found of a working NDR computer ever constructed.
Though a huge pile of moldy-old research papers and related patents persist.
Once was an NDR-Klein computer kit, but the letters were just a coincidence.
Not same thing as "Negative Differential Resistance" at all...

 

[Derfnofred]

I have only just looked at your ltspice diagrams and plots, but one thing that should be noted is that anything magnetic isn't going to scale to densities that are comparable to present binary logic, even with respective advantages.

Memristor covers a few different technologies, but essentially programming in a variable resistance.

 

[KD5ZXG]

Spin torque MRAM isn't quite competitive in density yet, but improving...
Wipes the floor of every other true non-volatile tech for infinte fast writes.
https://www.everspin.com/64mb-spin-torque-mram-ddr3-dram-compatible

I got one of their 16MBit parallel bus devices to use as a huge ALU table.
Enough there to pack every imaginable 8bit vs 8bit operation with plenty
left over for flags and user space. But that project is a whole other rant...

The old Parametron donuts weren't non-volatile like CORE or MRAM.
Soft inductors would forget immediately. Such logic held memory only
in the phase of an oscillation. A self-refreshing dynamic ram of sorts.
I'm not suggesting go back to those, except they are fun to play with.

Was only to illustrate gateless, oscillating, majority logic. That for nearly
a decade, real computers were successfully made of. Mostly to break
you free of thinking gates and transistors are the only tools to compute,
or even essential. I wanted to show you something completely different.

Also may be "magnetic", but the new Quantum Flux Parametrons
don't oscillate like ye donuts of old. I don't fully get exactly what a
Josephson Junction does, or how small they might could be made.
And I might be wrong, but I imagine its some kinda flipflop of spin?
-edit- nope, AC pumps Cooper pairs as DC supercurrent tunnels a
gap, but DC can flow round the gapped loop either direction 0 or 1.
Not exploiting electron "spin", but the loop current makes a flux.

Nothing wrong with transistor gates where those devices work best.
Just don't see them working too well all by themselves when the shit
gets quantum. Plenty of other options exist along side, that together
with gates might stretch what is possible in our near future. I'm mostly
interested how we make a working computer with those other logics.
Not limited strictly to gated logic we already know too well.

One other thing bugs me about quantum logic: Why exactly does one
need cold to make quantum work? My thoughts often return to magnetic
reconnection events in the Sun. A quantum computer instantly solving
the incredibly complex problem of finding a lower energy state. Clearly,
neither small nor cold was ever the requirement.

 

[Derfnofred]

As to the quantum logic portion: we need to cleanly identify shifts in electron energy states at extremely small charge volumes, so any smearing of that due to thermal variations (have a good read on Bose-Einstein statistics https://en.wikipedia.org/wiki/Bose–Einstein_statistics), will swamp out the underlying probability function given by the quantum logic.

And, holy crap, it's been years since I've had to look at Bose-Einstein equations.

 

[KD5ZXG]

You are obviously correct for cold single quanta where half a spin matters, but that sort of
logic is simply not practical outside of a lab. Practical quantum needs redundancy and error
correction, and a majority of votes easily offers both. Don't have to count the exact state of
single electrons per input to leverage quantum effects. Smeared quantum works fine too.
ie: Tunnel diodes at room temperature.

 

[KD5ZXG]

This is a spintronic majority logic device. Not yet sure if it works in only one direction like a gate, or any direction
like a Parametron. I see no intrinsic mechanism whereby the result would be amplified and maintained, so I am
leaning more toward gate.

Also couldn't find any specific detail how electrical signals at the SMA connectors are coupling to spins in the waveguide.
Guessing maybe STNOs (Spin Torque Nano Oscillators). http://www.akermanlab.com/spin-torque-nano-oscillators.html
Or could be circularly polarized, corner fed patch antennas. But why fed across to the far side of each waveguide branch?

And here with the ubiquitous pitchfork gun again. Are we seeing an actual circuit component? Or was this a photoshop
to explain something unseen? I can't tell from what little isn't hiding behind academic paywalls.

 

[KD5ZXG]

Lets review: There are three primitive uses (MAJ, AND, OR) for a Majority gate. Not counting clubbing baby seals.

-edit- Image replaced due to an error at bottom left gate, fixed now.

When we upgrade to Parametrons, we are no longer tied to transistors and gates.
But now we have to deal with a three phase clock, and this can be a true PITA.
Sometimes drawn as circles to emphasise no distiction between input and output.
The smaller circles represent inverted wire pairs.

Five Input Majority might be considered another case of primitive use. But like seals, it gets messy...

-edit- On futher consideration: Ideal padding per phase of addition might be Three, Five, Five.
The drawing stands for now, as only the text was incorrect. I might replace it later.
I've already figued a trick (detailed in a later post) to get rid of most of the padding.

Input and outputs want to occur all of one phase. But ripple carry wants to happen on every phase.
And we don't want to delay ripple. A final answer for ripple Carry requires the most steps to complete.
Delay almost anything else to achieve alignment with Carry is preferrable.

Adders that don't ripple are an entire other topic. (I'm into MRAM Lookup Tables and Carry Select.)
Won't be making any adders of oscillating donuts, except to understand the concept. When nano,
spin, quantum, whatever bizarro logic beats Morre first, we will be ready to deal with it.

 

[KD5ZXG]

Forgetting on every third cycle seems wasteful. Here: Thirteen Parametrons were wasted just
to align the phase of a 3bit, 9Parametron adder. If we could hold-off forgetting till the ADD was
complete, it might not need so much padding.

Perhaps a 9 phase clock (forget on every 9th phase) would give us enough hold-time to complete an 8bit
ADD without an absurd amount of padding? This might still be compatible with a 3 phase clock elsewhere.

Even a four phase clock (remembering for 2 phases rather than one) would elimate all but three of the
delay parametrons in the above drawing. Would a five or six phase clock make sense, or just go for 9?

 

[KD5ZXG]

I find no historical precedent for it, but it looks like a 9phase clock (forget, vote, hold, hold, hold, hold, hold, hold, hold, hold, hold) might work.
Or does 8bits require 10 phases? Yeah, I prolly screwed it. Only 7 parametron groups would be in a state of hold. Vote phase doesn't present
a useful output because the next group has to be in forget mode, else it might mistake output for an input.

So, 10 phases for 8bits, 6 phases for four bits. But I'm not fixin this drawing today....
I'm saying the parametrons of group2 in this drawing should be forgetting at time the output is read.
Everything from group3 and to the right should be holding a valid output.
A new input is forming at group1, unseen to the left of the drawing.

Did I screw this massively? Look at Group2 "output" C2. That parametron can't vote because Group4 is awake
and trying to turn that output into an input. Will require an extra forget phase added for every hold phase added.
9 Phases would yield only four bits in a valid state of (forget, vote, hold, hold, hold, hold, forget, forget, forget).
Eight of the seventeen input bits, & four of the nine output bits need hold to be stretched by a delay parametron.

12 wasted parametrons added to 24 that actually compute something isn't bad as it could be. But going to a 17
or 18 phase phase clock to avoid those wasted components seems like it could slow down a lot of operatings
that have nothing to do with ripple carried ADD, SUB, or Shift Left Arithmetic.

One would hope that Programmable Majority Arrays could someday be written in VHDL, just like FPGAs.
Let all this phasing nonsense be a problem for the compiler. Still, some Japanese dude from the 50's must
have figured it all out on paper. Except in Japan they didn't even have the "50's", they had the "Showa Jidai".
Plenty of evidence that Parametron Computers worked with a very reasonable quantity of primitive devices
and not huge amount of waste. Somehow in only three phases, without even knowing which decade they
were living in. Go figure...

-edit- I couldn't stand the above incorrect drawing any longer, but I leave it to show what can go wrong:
After half a dozen failed attempts, this drawing might even be error free now! Just don't count on it...

Timing should now be correct for 9 Phases (FFFFVHHHH) Forget, Vote, Hold.
The pattern is backwards if we examine what each group is doing.
Group 1 2 3 4 5 6 7 8 9 1
Phase1 HVFFFFHHHH (Simultaneous valid inputs are assumed to be held by Parametrons of Group1, not shown)
Phase2 HHVFFFFHHH
Phase3 HHHVFFFFHH
Phase4 HHHHVFFFFH
Phase5 FHHHHVFFFF (Neither inputs or outputs are awake right now, but somewhere in the middle we got this)
Phase6 FFHHHHVFFF
Phase7 FFFHHHHVFF
Phase8 FFFFHHHHVF
Phase9 VFFFFHHHHV
Phase1 HVFFFFHHHH (Valid outputs are now held by Parametrons of Groups 7,8,9,1)
All Sum bits and the final Carry can be simultaneously readout now.
If we wait to any longer to read, bits held by Group7 will be forgot.

Is there any way I could possibly have made that more confusing? I don't think so...

This phasing might also solve some timing problems of the 5 input Majorty adder.
If so, could we rip out eight Parametrons and still arrive at the same answer?

Nah, one intergroup connection (The X128 input) would then stretch one phase too
far without adding another holder. What's the point of saving one only to burn one?
But seven Parametrons could be saved.

I don't think anything nano, spin, or quantum does 5input, the savings would be irrelevant.
If you are building an old fashioned Parametron, or flipflops, 5input probably saves parts.

 

[KD5ZXG]

This is a real 8bit Majority adder. Whatever they are doing is different than what I drew.

Logic blocks at every input pair look suspiciously like Propagate & Generate.
We may be seeing some variant of Carry Lookahead.

Examine the right side, you see a wasteful column of at least 9 do-nothings.
I suspect at least half the devices in this photo do no logic, only align phase.
A few more phases could make this a lot smaller, maybe even use less power.

More than a few things seem a little off about this adder.
While I clearly see 9 pins output, I don't see any pin dedicated to a carry input.

Also counting clock rows, I see 6 cycles of three phases. Thats like 18 phases
of clock to avoid a ripple carry that should only have taken 9 phases? Shit, they
coulda rippled 16bit addition in that same length of time, with a phase to spare.
This what happens when you let supergenius go unsupervised...

 

[KD5ZXG]

If this drawing were traditionally 3 phase clocked, a Parametron would be needed at every dotted/solid intersection.
Pardon that some overlapping Parametrons might look like current sources, no symbol of that sort was intended.
Also not intending to show any special interaction, just cramming for vertical drawing space.

A nine phase clock can HOLD valid data for as many as four phases. Only 12 do-nothings needed.
Which still seems a large quantity of waste considering no more than 17 doing any actual addition.

Suppose X128+Y128 had saved ONE Parametron by upgrade to MAJ5, like other bits of this adder:
TWO do-nothings would be needed to stretch its input HOLD times. Which is why the final adder
was drawn using MAJ3 method. -edit- I've just noticed same issue affects X8+Y8. Those two inputs
won't HOLD quite long enough to reach Group 5. So this drawing is still slightly broken.

For three phase clocks and ripple carry, bit serial addition might have made better sense.
3bits at a whack, and roll the carry back into the input. Any size numbers could be added.
Still waiting on final carry, so a serial operation isn't going to be any slower. And presents
a much shorter pipe to pad with do-nothings...

I might try a "carry select" adder next, see if that might shorten the pipe. Basically, the low four bits
would be computed exactly as above, by ripple. So too would the upper four bits, except twice.
Once on speculation that there will eventually be a carry at C16. Also a parallel speculation that
there will be no C16. At the end, the wrong answer gets thrown out. No need to wait for C16 to be
known to start work on those upper bits. Speculative adders can move to the front of the pipe and
save on padding, maybe enough to offset the added logic.

 

[KD5ZXG]

Seven Clock Phases (Vote, Hold, Hold, Hold, Forget, Forget, Forget)

A 9th bit of addition could have been squeezed into these 7phases.
Drawing would have been too wide to fit on one screen though.

Hard to say exactly how many devices "wasted", I count at least six.
But one speculative third of the work is thrown away by carry select.
If the job gets done 2 phases faster, does that work count as waste?
Maybe not wasted, though some extra power definately burned.

I think the component count here might be 57 Parametrons.
How many do we count in the real 18 stage device of post #27?

 

[N4CR]

And its not just about the 1950s. Majority logic has been done in pure light.
Look Ma, no gates!!! Ok, so maybe it has a lid. But no gates, no wires, no
transistor. Light doesn't seem small or practical yet, but maybe someday.

View attachment 54180

At scales so small that transistor gates stop working, majority logic still gets
the job done. Thats why we might spend a few moments rediscovering it.

As long as the length/pulse timing isn't an issue I could shrink that optical layout to something that would fit in your palm.. further optimisation could get it down below CPU size easily.

Fascinating thread btw, still reading though Love quantum tech and this is quite similar. Thank you!

 

[KD5ZXG]

Muntzed quite a few of them donut thingies.
https://en.wikipedia.org/wiki/Madman_Muntz
Including outputs but not inputs, I now count about 50.

I've also come to realize that filling in all blank places with do-nothings isn't a waste.
Allows three phase timing, which in this 7 stage adder means 2 and a 1/3 sums could
be in the pipe at once without stepping on each other's weenie. By phasing as drawn,
parts are definitely saved. But enough to build another x1.33 to operate in parallel???
Yeah, maybe that much and more...

Not saying I know any simple way to take advantage of such a pipeline, only that
with all blanks filled and the right kind of clocking, that feature might be exploitable.
Each math is separated by a solid wall of forget. Same thats driving the logic forward.
Forward is downward in this drawing, if that wasn't obvious, and maybe it isn't...

When we start programming arrays of these on a chip, every place in the array will be
populated, weather we use those devices or not. So, pipelines may be a freebie if only
we can figure how having them helps in some way. Its not like extra parts would need
to be wasted.

 

[KD5ZXG]

My Japanese sucks. Don't even have a keyboard, and that can't
be helping. I lean on copy/paste and Google translate too much.
I still havn't gotten replies back from any of the dudes who know.
One congrat on getting the 150KHz donut to work, but no info.

They needed 18 steps to do a seven step job, but WHY?
Can't help but think I've missed something important.
Just occured to me what it might have been.
No resistors to help isolate fanout!

Assume all wires are resistors. Maybe on a cold chip they aren't?
If so, a do-nothing buffer might then be needed after every split.
Else, what separates logics that share a net? What keeps them
from locking together and performing one mututal operation?

That rolling wall of FORGET that pushes logic forward might be
all that prevents fanned I/Os from afflicting each other. Fanout
may be limited too. How many inputs can one output drive?
Hoping someone will chime in with the actual rules for quantum.

Its obvious on the real chip that some outputs must have split, but
exacly how do you split a quantum? I thought that was impossible.
So, like the case with tunnel diodes, I think we are seeing a mess
of quantum in parallel for each device. These seem to come in at
least three flavors, each quanta more quantum than the last:

DC Flux Parametron (Maybe what we've been looking at so far).
Adiabatic Quantum Flux Parametron, And Single Flux Quantum
Parametron. Without paying the walls, I'm not allowed to read
enough to determine if I'd even be able to understand.

--------------------------------------------------------

Even assuming the need for every resistorless split/mix to be
individually buffered, I still count only 14 steps. Probably not
fewer than seven phases if total component count matters.

Though I give 18 stage 3 phase design credit for being able
to jam *SIX* serially multithreaded operations into one pipe.
I didn't fully appreciate that feature existed on first glance.

A 14 step adder driven by 3phases might cram 4.66 adds
into the pipe, with four fewer stages of latency. Though it
might make better sense to throw a wasteful 15th stage
at this, for a more convenient whole number of threads.

If some other part of a complete CPU might need all of 18
stages? May be no point to a lower latency adder that holds
a mismatched number of threads.

 

[KD5ZXG]

Without a clear statement of the rules, I'm not ready to play the quantum game.
My latest attempts to scrape paywall leaks discovered only a 21 stage adder.
Up from 18, why now 21 stages? More than 2000 Josephson Junctions. And
they seem mighty proud of it too.

So, let's look back on another practical example of a real parametron computer.
From a day when 21 stages to add 8 bits would have been an appalling waste.
No such waste to be seen here. Though they threw a lot more vacuum tubes at
it than seem needed. Perhaps interface to other devices, such as core memory?

Hitachi Hipac MK1

On the right we see pairs of tubes with hoods that don't appear to help ventialltion.
Can't imagine any use for such a hood, unless perhaps nixies displaying numbers.
Except those look way too tall for nixies, and the tops don't appear flat. So I don't
know what the hell they were. Dekatrons? (Ring counter made of 10 neon lamps)
Except those were going out of style by the time of this machine.

To lower left, three huge pair of valves might be rectifiers, possibly mercury vapor.
Just above them, three quartets of beam power tetrodes with sparkplug tops.

I got some like that in my guitar amp (world's most dangerous plank) in storage.
Can't remember the number, but was like a higher voltage rated variant of 6L6.
-edit- 6BG6 was the beast I was thinking of, plank not necessarily this computer.
So, maybe this one??? Mine are near identical, but not Hitachi...

Clocks need DC bias, so the usual output transformer could have been omitted.
I think we are seeing about 200W output power per each of three phase clocks.
The consumed power would definitely have been higher than output.

-------------------------------------------------------------------

On each circuit card, we can see capacitors and magamps populate the front side.
Ferrite appears to have been formed as common 4 hole buttons, then sawn in half.
Nah, that shape has gotta be slightly more than half a circle. Maybe 2 hole button
with one side partially milled away?

You see a half button becomes two inductor donuts, wound on the flat side. And an
exciting clock line threads once through each dount hole in the opposite direction.
Each bucking the other to cancel out any direct transformer action. Only trying to
overdrive the thin-shaved edge of the buttons, and and thereby lower inductance.

Inductance needs to be lowered twice per cycle, to amplify and sustain oscillation.

The back was populated by I/O coupling donuts. But more interesting is the
clear grouping of three phases I, II, III. Hitachi etched them so, on the left.
Regular donuts take a lot more power to overdrive than the thin edge of a
button, which is why this more common shape wasn't used for both sides.

On the right, we see 6 thick pins for driving the three clock phases.
Current goes in, current comes out, so six pins to handle three clocks.
Clocks were DC, never conducting backward. But the amount did vary,
twice per resonant cycle, so DC+AC(2f)...

I'd be furious at whoever bent those middle pins, cause this card looks like it would still work.
I count 20 differential pairs of I/O. Not enough I/O pins for a fully populated card. Each card
must have been customized for a specific function. I don't see any resistors. Those might be
hiding somewhere behind the backplane?

I suspect quantum needs so many stages because it uses no resistors to split and mix I/O.
But no-one so far has come forth to clarify whats really going on...

 

[KD5ZXG]

For quantum, I think maybe something like this may be going on?
Logic seems to be fighting it out in manifolds inbetween latches.
Not much different than logic fighting it out in a resistive mixer,
except output splits sometimes require a dedicated extra step.
Else input manifolds that share an output would short together
and make nonsense.

For example, again we will abuse the 1Bit Full Adder

-edit- Messed up left full adder, the one made of entirely of inverters.
I shoulda downvoted MAJ5 by two carries instead of upvoting by two.
With only three phase drive, there is no way to align inverted inputs
with noninverted. With five phase drive, I'd have the option to skip a
step, and then X,Y,Z,C/,C/ or X/,Y/,Z/,C,C could be properly aligned.
Either alignment would have let me compute a proper Sum or Sum/.

Don't worry bout step 4 not drawn above. As we ripple carry more bits, it will get used.
5 phases permit two steps behind each vote to remember, while two steps ahead forget.
Else each vote (in a 3 phase system) could only reference the most recent prior state.

Clearly we didn't need real inverts when a mirror universe exists next door.
Clearly we don't need a mirror universe when every step inverts the whole
machine, and we have an option to reach more than one step back in time.
If inverting is optional for every device, there was no problem to begin with.

Probably should bust out an extra copy of C and C/ at stage 2,
so we don't waste time splitting those again for the next bit.

Suppose Z is our carry input. See where Z splits at stage 1?
For the next bit we can skip that split entirely and minimize the
latency for carry to ripple through. X and Y of the next bit can
also split one step ahead of time, since they don't need to wait
for carry.

--------------------------------

Dunno if Josephson Juntions can invert, always invert, maybe its optional?
What I can make of photos don't seem like they've been trying the mirror trick.
Nor have they been taking advantage of 5 input majority, maybe they can't?

I still don't fathom why 21 stages for an 8 bit carry lookahead adder.
Especially when they had proven an 18 step adder just a few years ago.
Does not compute! No more than 9 stages should be needed even with
the least efficient ripple. As shown before, speculative carries offer even
lower latency. I would expect seven stages to be no problem.

Maybe a patent thing keeps them from adding more efficiently?
They did hit 5GHz on the 21 stage adder, gotta give em that.
And likely with seven ADDs simultaneously in the pipeline.

-edit-

This blurry thumbnail answers at least one of my questions.
Maybe two...

Looks like JJs can be made to do either job: invert or non-invert
So, there is no need for a duplicate inverted machine.

Also seems able to cast constant votes. AND clearly got a local
zero vote thrown into it, yet we count no extra wire for that vote...

I still don't know how many ways one output can split
before getting into trouble, nor how many inputs max.

I imagine lower fanout would be faster, even if higher
fanout works, & lower fanin less susceptible to noise.
But thats just me imagining things...

With optional inversion at any step, full addition can be computed
in just three steps. With the first carry ready to ripple in two steps,
because carry input still needs a step to split. Subsequent carries
can pre-spit and ready to ripple in one step.

If a pair of pre-split carry-ins were presented to the input terminals,
even the first bit's carry could be known in just one step.

 

[KD5ZXG]

I need to buy an old book "Advances in Quantum Flux Parametron Design" by Goto and his team.
From what little I can preview on Google Books, he had an 8bit adder that worked in just 5 steps.
And was doing so at 10GHz! Makes recent efforts of 21 steps at 5GHz seem very backwards...

Lets also assume FA on the right allows for a carry input, as every other FA in this drawing does.
-edit- Wouldn't work. Carry lookahead would have to know that input too, and use another step.
A "Co" input cannot simply be tacked onto this drawing.

Goto used Josephson Junction pass-though logic called a "Double D-Gate" to do it. Thats where
I am drawing a blank. Need to know how that worked. Seems more related to Parametrons than
gates despite the naming. Was something his friend Takahashi came up with in 1968, so I don't
think it depends on Josephson Junctions to work. Did they even have superconductivity in 68?

-edit-

Superconductivity was discovered tomorrow (April 8th) 107 years ago (1911).
And Josephson Junctions might have been possible recently as 1962.
So, D-Gates could be just a JJ thing? I'm still slightly in the dark.
https://en.wikipedia.org/wiki/Josephson_effect

Previews of different editions are missing different pages, still maybe enough info...
https://books.google.com/books?id=ZZ7sCgAAQBAJ&pg=PA143
https://books.google.com/books?id=euk7DwAAQBAJ&pg=PA21

Seems like I've been flogging the 8bit adder circuit to death, but at least it
helps when comparing pineapples to pineapples.

 

[KD5ZXG]

An issue of concern for resistorless coupling is how do we couple
logic devices without locking them together as one lumped vote.
But Takahashi's D-Gate seems to turn this problem to advantage.

Suppose a pair of Parametrons driven by insufficent excitation.
Each passing no signal to a mutually coupled output. But we will
choose to give one a little extra drive. That one quickly reaches
self-sustaining gain, and the weaker will latch in symapthy. Thus
we might make a Multiplexer. D-Gate appears to be such a device.

The excitation signal to unblock a chosen path comes not entirely
from the clock, but from two other Parametrons of the same clock.
So, decisions within a D-Gate are not entirely synchronus. But a
final answer is held to the clock, just like any other Parametron.

Two signals that will direct the Multiplex are amplifed and then
differenced by output coils wired out-of-series. From here a diode
bridge may have been used. As that would restore both DC and the
double frequency needed to open one of the blocking Parametrons.

Of course, the same may be done for output coils wired in-series,
to drive open the other path. Which path will open depends wether
the directing signals are in-phase (both zeros, both ones), or out of
phase.

So, we have a total of four inputs: X Y, only one will be passed.
Also W Z, which choose X if they are the same, else they pass Y.
All this boils down to one latched output.

---------------

This tricky gate can be wired up for CARRY (same as MAJORITY).
Seems a waste, since a single Parametron could already do that.
But can also be wired PARITY (same as SUM) in the same cycle.

Actually its not a waste to use D-Gate for MAJORITY, as it buffers
mutual coupling problems without burning an extra stage to do it.

D-Gate can also be wired for Carry Lookahead functions such as
GENERATE (same as AND) or PROPAGATE (same as OR). One
pair of W Z input buffers is said strong enough to drive two blocking
pairs, making the Double D-Gate.

Double D-Gate could also be made of a DPDT relay. If that helps to
understand the function any better. Wouldn't surprise me if the idea
somehow evolved from them. Even Goto's schematic symbol for it
looks suspiciously like a relay.

Hopefully, I got that right, cause only so much of 1968 can be dug
out of Archive.org . The rest I'm having to re-imagine as I go. Not
to worry! I'll post some highly misleading drawings later, and this
terrible explanation will make even less sense...

---------------

Attached some detail about quantum D-Gates around Pg6, not so
much the earlier LC style that Takahashi might have built.

Almost of greater importance might be FLATS2. No, that wasn't a
Quantum Parametron, it was ECL. But was testing some pipeline
concepts they wanted to apply. Three years before Windows95,
and they were already benchmaking a cyclically multi-threaded
machine with 12 operations in progress in two pipes!

And it wasn't just a stupid round-robin either. Compiler could flag
instructions of the same thread that didn't have to wait thier turn.

 

[KD5ZXG]

Seems our Quantards re-invented the Double Pole Double Throw Relay! Go figure...
Double D-Gate I mean. Two gates sharing one drive pair, else would be Single Pole.
Took me weeks just to figure that out. Fortunately, designing with them is a lot simpler.

When inputs located on the side agree, the mux arrow points as drawn on the symbol.
When inputs located on the side differ, the arrow re-aims to the normally open position.
For sake of uncluttered drawing, let side inputs also pass through to the other side.
If I was drawing a Double D, probably just stick them side by side w. implied wiring.

Note: XYZ order doesn't matter for MAJORITY, CARRY, SUM, or DIFFERENCE.
But XYZ order definitely matters for BORROW. Because X represents a positive
starting number that negative numbers Y and Z would be subtracting away from.

AND and GENERATECARRY are exactly identical operations.
OR and PROPAGATECARRY are identical.
MAJ and CARRY are identical.
SUM, DIFFERENCE, and PARITY are identical too.

XOR is just SUM with an input stuck at zero.
AND is just MAJ with an input stuck at zero.
OR is just MAJ with an input stuck at one.
Any one input could serve as the stuck input, doesn't matter which one.
Where I've drawn X and X/ going into SUM, together count as one input for this rule.

D-Gate isn't exactly a mechanical relay. Relays behave like gates. Inputs need to be held
valid until the final output has been read. Unless synchronous latch and forget behaviors
could be mechanically or electrically added to break a relay process into stages, they
would not automatically form a pipeline.

Relays have different rules about what constitutes shorted IO. And don't always present the
opportunity to invert for free. Might need extra inverter relays which add even more delay.
A parallel opposite machine, or full differential operation may avoid those inversion delays.
But double the contact count would also be double opportunity for a mechanical failure.

D-Gates get around all those problems. Free inversion. Latch an answer at each stage.
Clearly very different, yet too many similarities with Relay Logic to be mere coincidence.
The updated drawing above shows very much what similarities I'm talking about.

How best to make a test D-Gate of donut or shirt button Parametrons, as Hidetoshi Takahashi
might have done it? I can guess, but I've found no schematics to prove. Josephson Junctions
are out of the question for me, so can't directly follow Goto's lead either. And no, I'm not going
to build any test circuits out of relays...

 

[KD5ZXG]

One of the references mentioned in JPRS papers:

Takahashi (edited), "Parametron Computer," Iwa-nami Publishing, 1968.

That's probably what I'm looking for...

May have to resort to searching in Japanese. I'm no good at it.
Teacher once kicked me out of class for saying "Kimi", and I'm
thinking "Isn't that also the 1st word of your national anthem???"
Was better off learning from toons.

 

[KD5ZXG]

Still digging for Takahashi clues in old books.
Wasn't exactly what I was looking for, but couldn't pass:
The First Computers - History & Archetectures (MIT)
Majority gates seem to have been in use well before Takahashi or Goto.

Those inhibit lines could have been useful for clocking a pipeline.
I don't have any clue if thats what they were actually for though.

Doesn't say what Turing's take on inverters might have been.
Seems you could input a constant 1, then maybe inhibit it.
That would be an inverter of sorts...

Suppose Turing's inhibits were not absolutely inhibiting, but a
balanced set of inverting inputs. Text above suggests they were
absolute, but has the author interpreted this symbol correctly?
How else might the threshold value of "m" have been set?

Goto used the exact same symbol as Turing. Except the side channel
of a Parametron excites, rather than inhibits. The Paragraph suggests
Von Neumann also used this symbol. Does that mean EDVAC used
majority logic? Damn, now I need that report too...

 

[KD5ZXG]

Today, Professor Eiiti Wada wrote me to correct my Romanization of names.
He also authored several pages of the MIT book above, and probably others
I have referenced.

To write "Hidetosi Takahasi" (Kunrei-siki system) could be more correct than
"Hidetoshi Takahashi" (Hepburn system) because that is how he preferred to
write his own name. I had never heard of either system before today.

Eiiti Wada and Eiichi Goto share the same first names, but have chosen to
translate the spellings differently. Eiichi Goto used Hepburn to spell his name.
It was explained that the learned elite prefer Kunrei-siki. So why then did Goto
choose the system for dummies like me?

Fortunately I have what little wreckage remains of my father's DIY 20MHz DTL
PDP-8/e compatible. Eiiti seems to be tripping hard on PDP-8 these days, so I
might be able to get a Parametron question or two answered in return.

----------

I now have 1st draft of EDVAC, and inhibit was absolute as the book described.
Later I'll attach a pic of VonNeumann's adder from that machine. Inhibit seems
a very difficult substitute for inversion and required more gates than it saved.
In some places inversion was used, but seems to be the exception. Its not like
he had a cheat sheet from a decade later to show an easier way.

Don't have Turing's ACE adder, but I have diagrams of MOSAIC that his team
put together shortly after. Appears to use pretty much the same sort of gate...

The circle with a 2 in it could have depicted a Majority gate. But neither seem to
have used it for anything but AND. Until I see an actual schematic of this gate,
there's just no telling.

-----------

Any inputs of AND that might be inverted would behave the same as an inhibit.
I think I've got my answer, and points more toward NAND gates, not Majority....
A twin triode could make two NAND gates, or a single AND gate (by inverting
the output), or NAND with an inhibit (by inverting one input).

Again this is guessing, how I might have done it, not based on real evidence.
Since VonNeumann suggest no more than two tubes needed per E-Element
(Turing called the same gate something else, I neglected to write down and
now can't re-find it). I'm thiking an input network of point contact diodes might
have performed the actual logic. Maybe thats cheating. Did they have some
other ancient insight on how to do AND without resorting to catswhiskers?

Another clues come from learning that Alan Blumlein worked with both of them.
So its likely we would see Blumlein's garter bias at work somewhere. Maybe
he was responsible for Turing and Neumann being on much the same page?
"Garter Bias" was a trick for adjusting tubes to match better.

https://www.tubecad.com/2005/May/blog0046.htm